出路WayOut ios版

出路WayOut ios版是一款经典的休闲探索类型的游戏，游戏中玩家将会享受更多趣味的方块，感受不一样的游戏世界，找到风快游戏的出路，享受游戏带来的魅力。

出路WayOut ios版特色

1、数学是Universal Language。无论是 3+4=7， III+IV=VII，还是:{{{，说的都是同一件事，真理是存在的。就3+4=7而言，请参考Peano公理系统。

2、我要学数学。

3、交换性/对称性是好东西。为什么古人觉得地球是平的呢?因为他们理所当然地认为自己所处的空间具有对称性——先往北走100米再往东走100米，等同于先往东走100米再往北走100米。实则不然，以后讲到HyperRogue时会详细探讨这一点。

出路WayOut ios版玩法

WayOut 是一个按灯的游戏，每按一盏灯会改变它及周围所有灯的状态，目标是把所有灯关掉。

它的原型是Lights Out，一款由Tiger Electronics发行的“掌上游戏机”。5*5的灯阵，总共有8388608个不同谜题，保证每次玩的都不一样！8388608=223，好像暴露了什么。

交换性体现在哪呢?按灯的先后顺序不会影响最后的结果，所以问题归结于“按哪些灯”而不是“如何操作”。做视频/GIF攻略的朋友辛苦了，但吃力不一定讨好，我觉得图片攻略更简明易懂。

如果有n盏灯，则总共有2n种按法，它们构成F2上的n维线性空间。和我们熟知的线性空间类似，只不过其系数取自有限域F2={0, 1}，其中0+0=0，0+1=1，1+1=0，etc。（可以理解为偶+偶=偶、奇+奇=偶，但一个域除了有加法结构还有乘法结构）

举个栗子，如图有A, B, C, D四盏灯。

2A = 0，即：连按两次A等于什么也没做。

(A+B) + (A+C) = B+C，即：按A和B，再按A和C等同于按B和C，因为A按了两次。

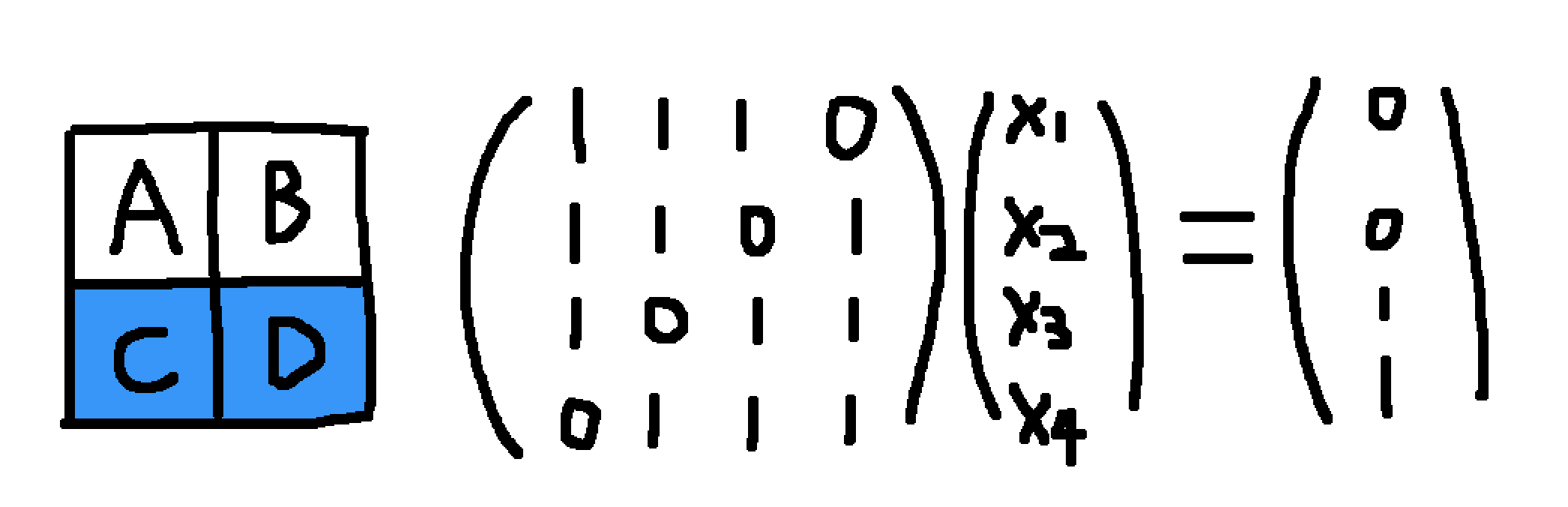
注意到：按A改变了A, B, C的状态，按B改变了A, B, D的状态，etc。因此左边的问题转化为解线性方程组。当然，是在F2上。解得x = (1, 1, 0, 0)——A与B各按一次即可。（注意：1+1=0)